Triángulos Inscritos en Curvas de Jordan

¿Será cierto que toda curva de Jordan admite un triángulo equilátero inscrito? Es decir, si \(J\subset \mathbb{R^2}\) es una curva de Jordan, ¿existirán tres puntos de \(J\) que sean los vértices de un triángulo equilátero? Pues resulta que sí, y la prueba de este hecho es sencilla:

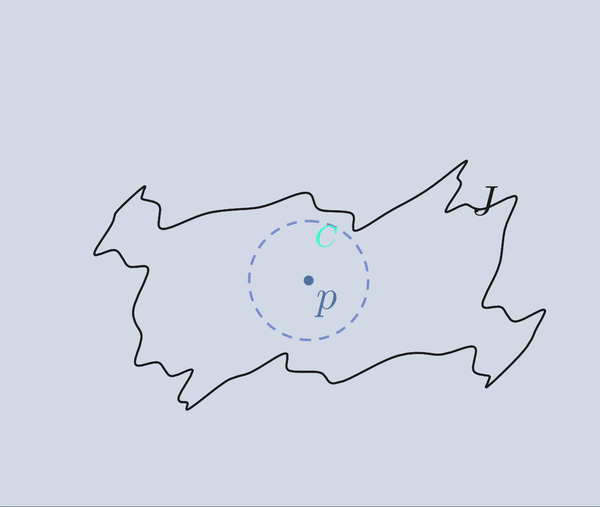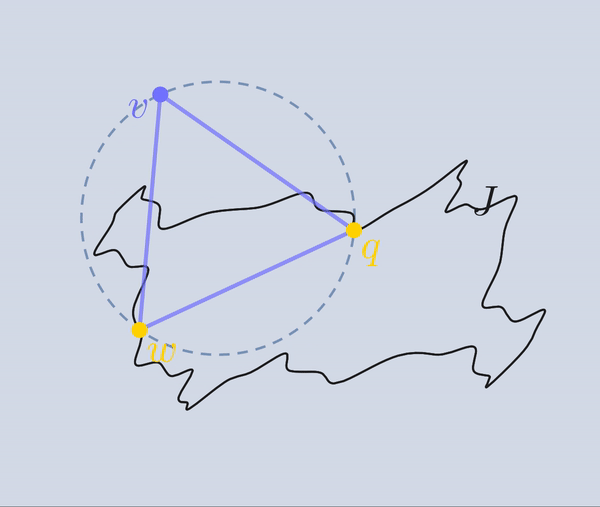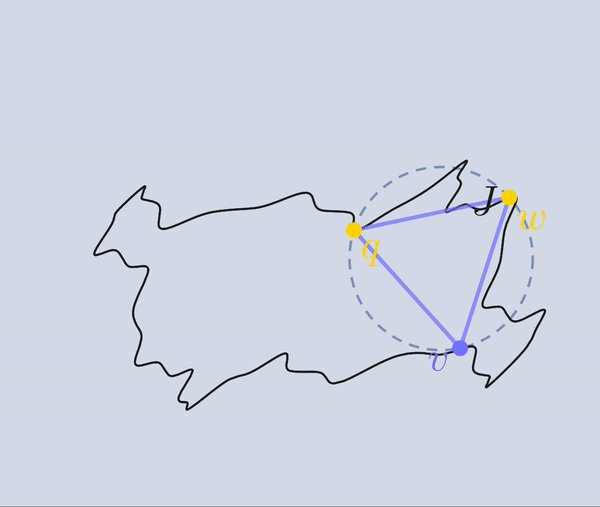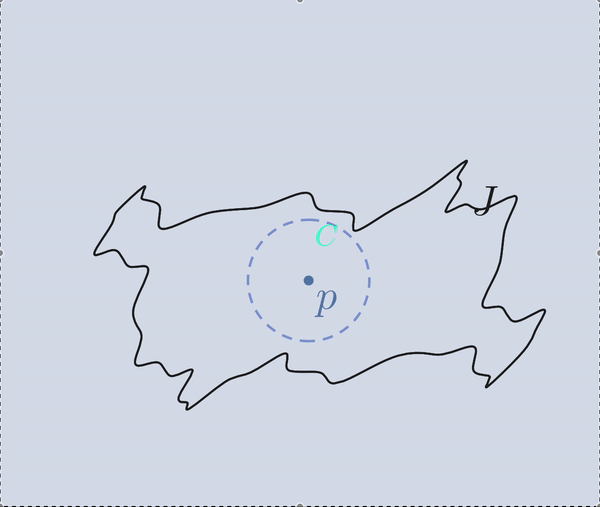
Tomemos un punto \(p\) en la región acotada de \(\mathbb{R^2}\setminus J\), que denotaremos por \(I(J)\); como dicha región es un abierto de \(\mathbb{R^2}\), podemos considerar una circunferencia \(C\) con centro en \(p\) que se quede contenida en \(I(J)\).

Ahora hacemos crecer el radio de \(C\) de manera continua y nos detenemos cuando \(C\) toque a la curva \(J\) por primera vez, digamos en un punto \(q\). (Bien pudo haber pasado que \(C\) haya intersectado a \(J\) por primera vez en más de un punto, pero no importa, elijamos uno de esos puntos y nombrémoslo \(q\).)

Consideremos el triángulo equilátero inscrito en \(C\) que tiene un vértice en \(q\), y llamemos \(v\) y \(w\) a los otros dos vértices. Notemos que nuestra construcción garantiza que tanto \(v\) como \(w\) (y de hecho la circunferencia completa \(C\)) están contenidos en \(I(J)\cup J\).

Si \(v\) y \(w\) están en \(J\), ya acabamos: \(q, v \) y \(w\) son los vértices de un triángulo equilátero inscrito en \(J\). Si por lo menos uno de los puntos \(v\), \(w\) no está en \(J\) podemos garantizar que existe un triángulo equilátero con un vértice en nuestro punto fijo \(q\), otro vértice en \(J\) y un tercer vértice en \(I(J)\cup J\). Pues si un vértice, digamos \(w\), está en \(J\), justo estamos en esa situación y si ninguno de los dos puntos, \(v\) y \(w\), están en \(J\), entonces hacemos crecer el radio del círculo \(C\), dejando fijo a \(q\) (i.e. moviendo continuamente el centro de \(C\) en la dirección \(\vec{qp}\)), hasta que otro de los vértices, \(v\) o \(w\), también esté en \(J\). Digamos que \(w\) es el primero de esos dos vértices en tocar a \(J\), y notemos que \(v\) sigue estando en \(I(J)\cup J\).

Si \(v\) está en \(J\) entonces, nuevamente, \(qvw\) es un triángulo equilátero inscrito en \(J\). Si \(v\) está en \(I(J)\), entonces, dejando fijo a \(q\), vamos moviendo a \(w\) de manera continua sobre \(J\) y nos fijamos en la trayectoria que va describiendo el vértice \(v\) del triángulo eqilátero \(qwv\). Notemos que \(v\) tendrá que cruzar la curva \(J\) en algún momento. Para convencerse de esto basta ver la animación que aquí incluimos, para demostrarlo:

Recordemos primero que, como \(J\) es un compacto de \(\mathbb{R}^2\), podemos encontrar un punto \(m\in J\) que esté a distancia máxima de \(q\) en \(J\), i.e: \[\exists m\in J\text{ tal que } \|q-m\|=\max\{\|q-x\|:x\in J\}. \] Resulta entonces que dado cualquier punto \(x\in I(J)\), debemos tener \(\|q-x\|<\|q-m\|\). (¿por qué? Sugerencia: use el hecho de que toda semirecta con punto inicial \(x\in I(J)\) debe intersectar a \(J\) en por lo menos un punto). Ahora bien, como \(w\) recorre toda la curva \(J\), llegará un momento en el que \(w=m\) y por por construcción, tenemos que \(v\) y \(w\) equidsistan de \(q\), con lo que \(\|q-v\|=\|q-w\|=\|q-m\|\). De modo que, cuando \(w=m\), tenemos \(v\notin I(J)\). Pero empezamos con \(v\in I(J)\), y la trayacyoria de \(v\) es continua: concluimos que en elagún momento la trayectoria de \(v\) intersecta a \(J\) y claramente en el momento en el que se da esa intersección tenemos un triángulo equilátero inscrito en \(J\).

La idea que acabamos de usar se puede generalizar para probar que las curvas de Jordan inscriben todo tipo de triángulos, es decir, si \(J\) es una curva de Jordan y \(T\) es un triángulo entonces \(J\) contiene los tres vértices de un triángulo semejante a \(T\) [1]. La prueba de este hecho es completamente análoga a la que acabamos de hacer para triángulos equiláteros, lo que cambia es que el triángulo que tomamos inscrito en la circunferencia lo tomamos semejante a \(T\) y de tal forma que el punto \(q\) corresponda al vértice con el ángulo más grande.

Ahora sabemos que las curvas de Jordan siempre admiten al menos un triángulo equilátero inscrito, pero todavía podemos decir más al respecto. En [1] Meyerson probó que dada una curva de Jordan \(J\), cada uno de sus puntos, salvo quizá dos, es un vértice de un triángulo equilátero inscrito en \(J\). En particular, este resultado nos dice que las curvas de Jordan inscriben muchos triángulos equiláteros y que el conjunto de puntos vértice es muy grande.

Además, en [1] Meyerson propuso que si \(T\) es un triángulo y \(J\) es una curva de Jordan que cumple ciertas condiciones de suavidad entonces el conjunto de puntos vértice de \(J\) es grande, como en el caso en el que \(T\) es un triángulo equilátero. En [2] M.Nielsen probó que si \(J\) es una curva de Jordan cualquiera (sin pedir condiciones de suavidad) y \(T\) es un triángulo entonces el conjunto de \(T\)-puntos vértice de \(J\) es denso en \(J\).

Referencias

Mark D. Meyerson. Equilateral triangles and continuous curves. Fund. Math., 110(1):1–9, 1980.
Mark J. Nielsen. Triangles inscribed in simple closed curves. Geom. Dedicata, 43(3):291–297, 1992.