Métrica de Hausdorff

Métrica de Hausdorff para $F_2(X)$

En esta sección veremos cómo se define la métrica de Hausdorff sobre el segundo producto simétrico de un continuo $X$, es decir sobre el conjunto que consta de todos los subconjuntos de $X$ con a lo más dos puntos, o bien, usando notación, sobre $F_2(X) = \{\{x,y\}:x,y\in X\}$.

Sea $X$ un continuo (i.e. un espacio métrico compacto y conexo con más de un punto) con métrica $d$. Para $\{x,y\}\in F_2(X)$ y $r>0$ definimos la nube abierta de radio $r$ alrededor de $\{x,y\}$ como $$N_r(\{x,y\}) := B_r(x)\cup B_r(y)\ ,$$ donde las $B_r$ son las bolas de radio $r$ con centro en $x$ y $y$ respectivamente (en $X$). Notemos que si $x$ es igual a $y$ entonces $N_r(\{x,x\}) = N_r(\{x\}) = B_r(x)$. 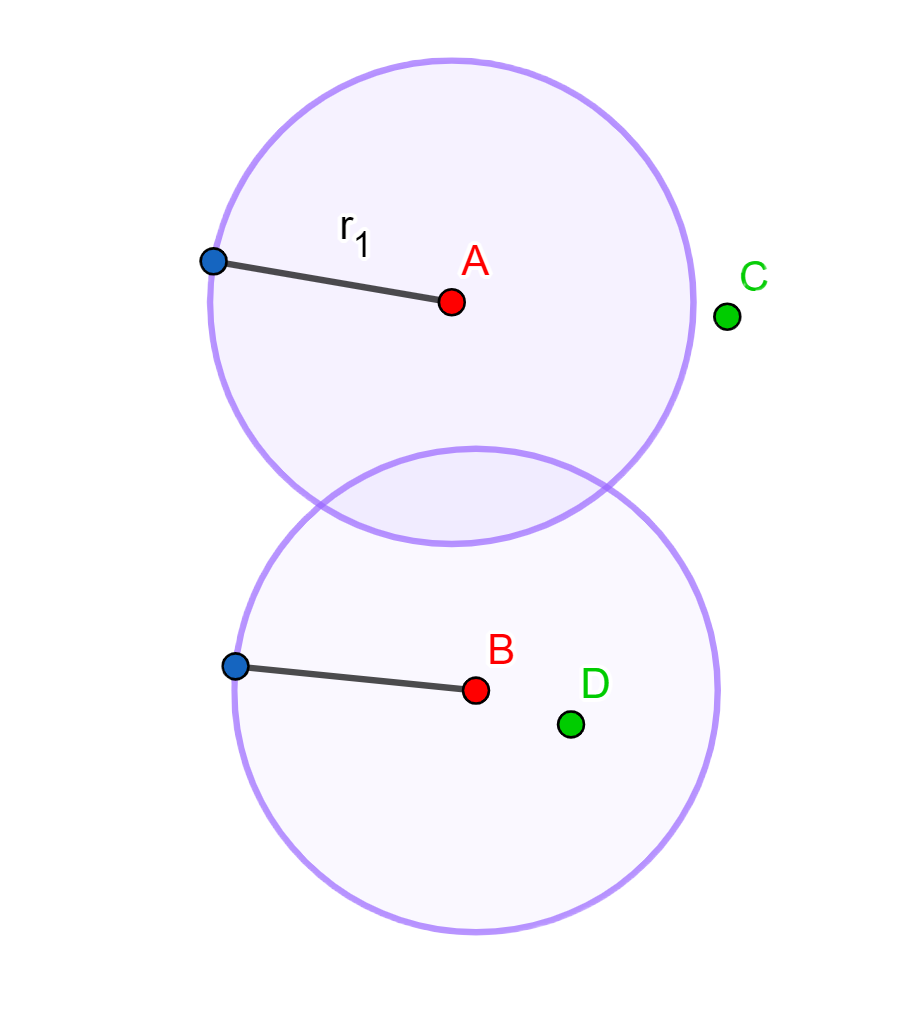Ahora sí, definimos la métrica de Hausdorff $\mathcal{H}:F_2(X)\times F_2(X) \to [0,\infty)$ como $$\mathcal{H}(\{a,b\},\{c,d\}) = inf\{r > 0 : \{a,b\}\subset N_r(\{c,d\})\ \text{ y } \ \{c,d\}\subset N_r(\{a,b\})\} .$$ Es decir, la distancia de Hausdorff entre $\{a,b\}$ y $\{c,d\}$ es el ínfimo de los números $r > 0$ tales que los puntos $a,b$ se quedan contenidos en la nube de radio $r$ con centro en $\{c,d\}$ y los puntos $c,d$ se quedan contenidos en la nube de radio $r$ con centro en $\{a,b\}$. Por ejemplo, en la siguiente imagen el punto $C$ no se queda contenido en la nube de radio $r_1$ con centro en $\{A,B\}$ (la región morada) por lo que la distancia de Hausdorff entre $\{A,B\}$ y $\{C,D\}$ es mayor a $r_1$. 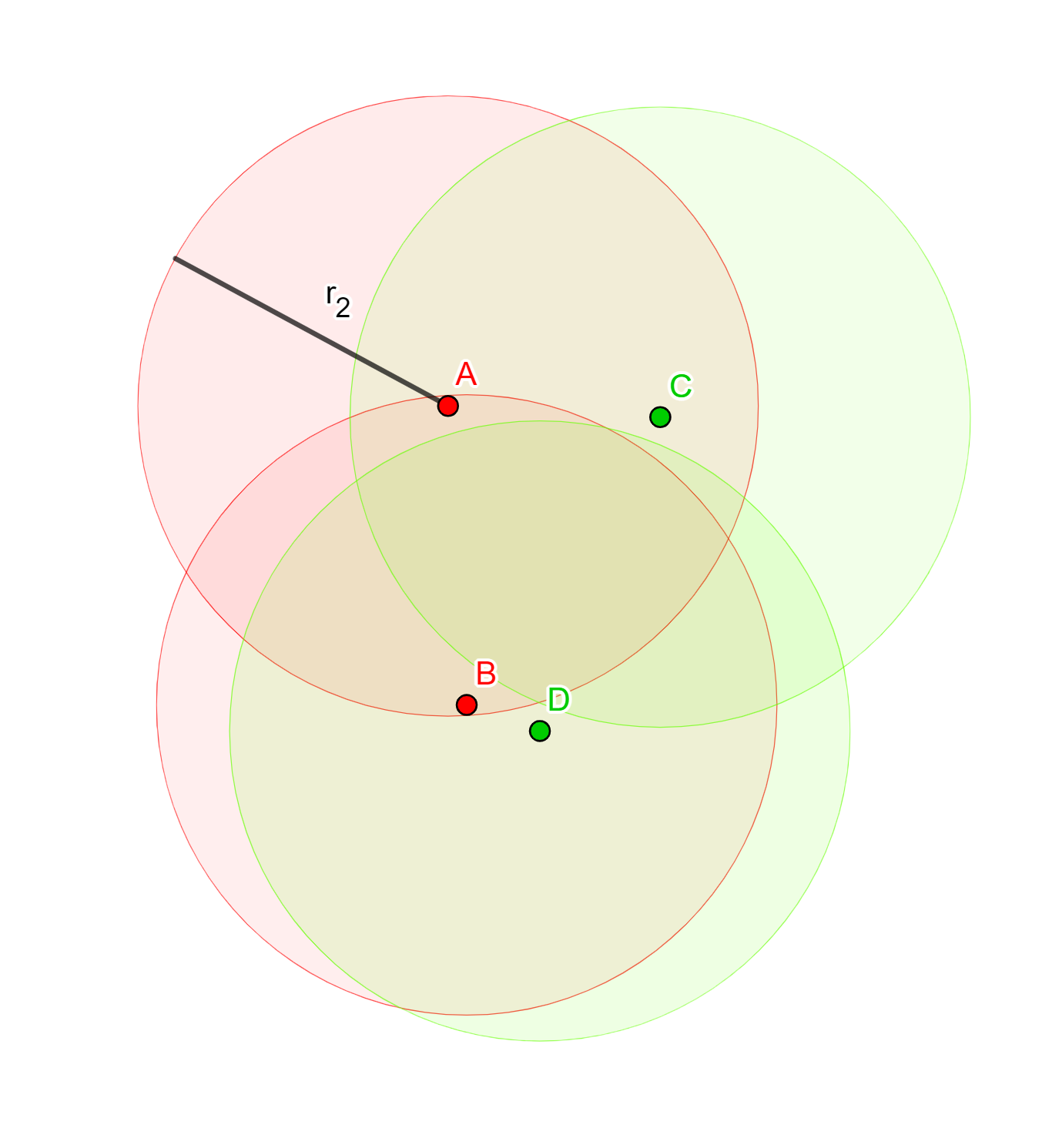Por otro lado, en la siguiente imagen vemos que $\{A,B\}$ se queda contenido en $N_{r_2}(\{C,D\})$ (la región verde) y $\{C,D\}$ se queda contenido en $N_{r_2}(\{A,B\})$ (la región roja), por lo que la distancia de Hausdorff entre estas parejas de puntos es menor que $r_2$.

Dejaremos para la siguiente sección probar que $\mathcal{H}$ es una métrica. De hecho, en la siguiente sección definiremos la métrica de Hausdorff sobre un conjunto mucho más general: el conjunto de cerrados no vacíos de un continuo $X$.

Métrica de Hausdorff (más general)

Sea $X$ un continuo (i.e. un espacio métrico compacto y conexo con más de un punto) con métrica $d$ y consideremos el conjunto $2^X=\{A\subseteq X: X\text{ es cerrado y no vacío}\}$. Para cada $A\in 2^X$ y cada $x\in X$ definimos la distancia de $x$ a $A$ como $$d(x,A) := inf\{d(x,a):a\in A\}$$ y para cada $r>0$ definimos la nube de radio $r$ alrededor de $A$ como $$N_r(A) := \{x\in X:d(x,A) < r \} = \bigcup_{a\in A}B_r(a)\ .$$

Definimos la métrica de Hausdorff $\mathcal{H}:2^X\times 2^X \to [0,\infty)$ como $$\mathcal{H}(A,B) = inf\{r > 0 : A\subset N_r(B)\ \text{ y } \ B\subset N_r(A)\} .$$ Veamos que ésta es una métrica sobre $2^X$.

Proposición: $\mathcal{H}$ es una métrica sobre $2^X$.

Demostración:

La simetría y la no negatividad se siguen de la definición. Ahora, veamos que, para $A,B\in 2^X$, $\mathcal{H}(A,B)=0$ si y sólo si $A=B$. Si $\mathcal{H}(A,B)=0$ entonces, para cada $n\in \mathbb{N}$ se tiene que $$A\subset N_{\frac{1}{n}}(B)\ ,$$ de modo que, si $a\in A$ entonces, para cada $n\in \mathbb{N}$, existe $b_n\in B$ tal que $d(a,b_n) < \frac{1}{n}$. Así, $\{b_n\}_{n=1}^\infty$ es una sucesión en $B$ que converge a $a$, y como $B$ es cerrado en $X$ entonces $a\in B$. Como $a\in A$ fue arbitrario, concluimos que $A\subseteq B$ y de manera análoga se prueba que $B\subseteq A$, de donde $A=B$. Para el regreso, si $A=B$, tenemos que $A\subset N_r(A)$ para todo $r > 0$, de donde $\mathcal{H}(A,B)=\mathcal{H}(A,A)=0$.

Sólo falta probar la desigualdad del triángulo. Sean $A,B,C\in 2^X$. Probaremos que $$\mathcal{H}(A,C) \leq \mathcal{H}(A,B) + \mathcal{H}(B,C)\ .$$ Sea $\epsilon > 0$. Sea $a\in A$ y $r=\mathcal{H}(A,B)+\epsilon$. Como $r>\mathcal{H}(A,B)$ entonces $A\subset N_r(B)$, por lo que existe $b\in B$ tal que $$d(a,b) < \mathcal{H}(A,B) + \epsilon\ .$$ Como $b\in B$, de manera análoga, existe $c \in C$ tal que $$d(b,c) < \mathcal{H}(B,C) + \epsilon\ .$$ De las dos desigualdades anteriores y de la desigualdad del triángulo para $d$ se sigue que $$d(a,c) \leq d(a,b)+d(b,c) < \mathcal{H}(A,B) + \mathcal{H}(B,C) + 2\epsilon\ ,$$ y así $d(a,C)<\mathcal{H}(A,B) + \mathcal{H}(B,C) + 2\epsilon$. Como $a\in A$ fue arbitrario, acabamos de probar que $$A\subset N_{\mathcal{H}(A,B) + \mathcal{H}(B,C) + 2\epsilon}(C)\ .$$ De manera similar podemos probar que $$C\subset N_{\mathcal{H}(C,B) + \mathcal{H}(B,A) + 2\epsilon}(A)\ ,$$ y como $\mathcal{H}$ es simétrica, esto es equivalente a $$C\subset N_{\mathcal{H}(A,B) + \mathcal{H}(B,C) + 2\epsilon}(A)\ .$$ De la definición de $\mathcal{H}$ se sigue que $$\mathcal{H}(A,C) \leq \mathcal{H}(A,B) + \mathcal{H}(B,C) + 2\epsilon$$ y como $\epsilon > 0$ fue arbitrario, concluimos que $$\mathcal{H}(A,C) \leq \mathcal{H}(A,B) + \mathcal{H}(B,C)\ .$$ Por lo tanto, $H$ es una métrica. $\square$

Métrica de Hausdorff

Métrica de Hausdorff para \(F_2(X)\)

Métrica de Hausdorff (más general)