Caracterización de rectángulos

Para este caso, definiremos a un rectángulo como un cuadrilátero cuyos ángulos internos son rectos y sus lados opuestos son de la misma longitud

$\mathbf{\text{Lema. }}$ Sean $A,B,C,D\in {\mathbb{R}}^2$. Si los segmentos $AB$ y $CD$ poseen el mismo punto medio $M$ y $|AM|=|CM|$ entonces $A,B,C$ y $D$ son los vértices de un rectángulo $R$

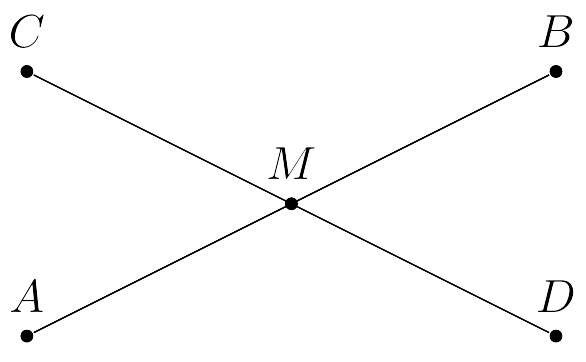
Sean $A,B,C,D,M,AB$ y $CD$ como en la figura superior. Por hipótesis tenemos que $|AM|=|CM|$ y, como $M$ es punto medio de $AB$ y $CD$ se sigue que $|MD|=|MB|$
Por el criterio $LAL$, los tríangulos $\mathrm{△}CMA$ y $\mathrm{△}BDM$ son congruentes.

Se sigue que $|CA|=|BD|$
Por un argumento análogo tenemos que $|AD|=|CB|$

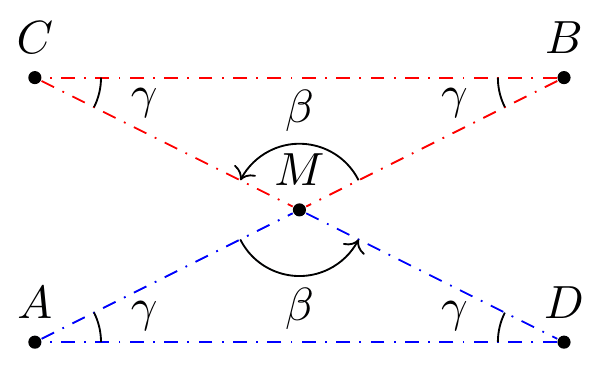
Observemos que
$$\begin{array}{rl}\pi & =\alpha +2\theta \\ \pi & =\beta +2\gamma \\ \pi & =\alpha +\beta \end{array}$$
De las igualdades anteriores tenemos que: $$\begin{array}{r}2\pi =\alpha +\beta +2(\theta +\gamma )\iff \pi =2(\theta +\gamma )\iff \theta +\gamma =\frac{\pi }{2}\end{array}$$ De lo anterior tenemos que los ángulos $\mathrm{\angle }CBD$ y $\mathrm{\angle }DAC$ son rectos

Lo que concluye la demostración del lema