Inscribiendo polígonos
Empezamos con un par de preguntas:
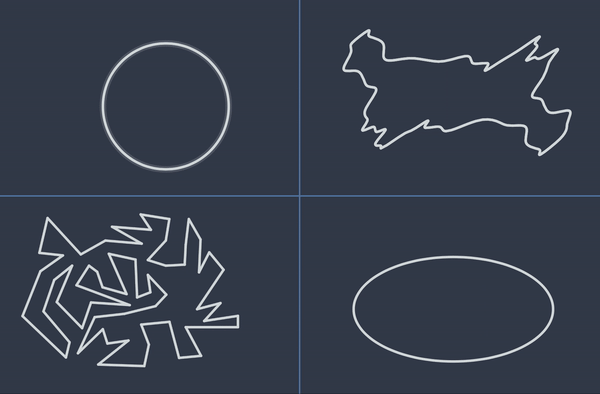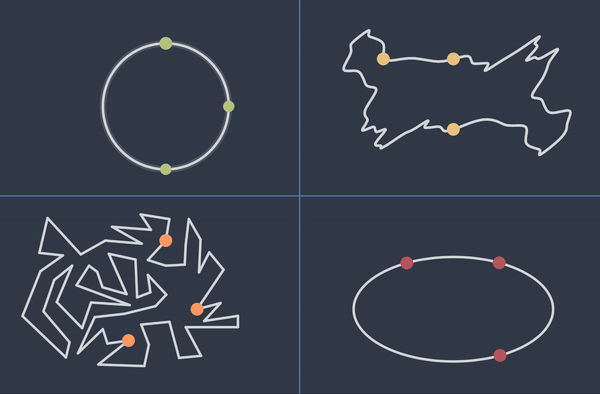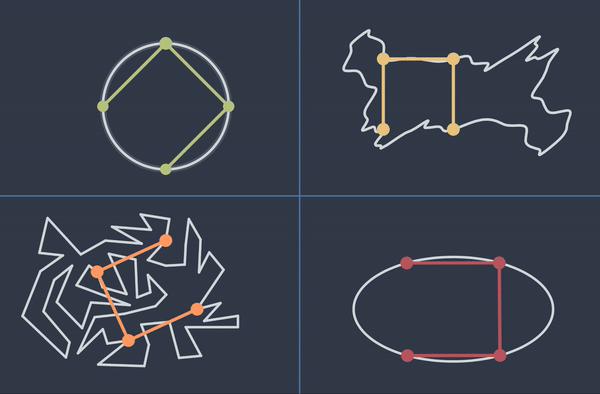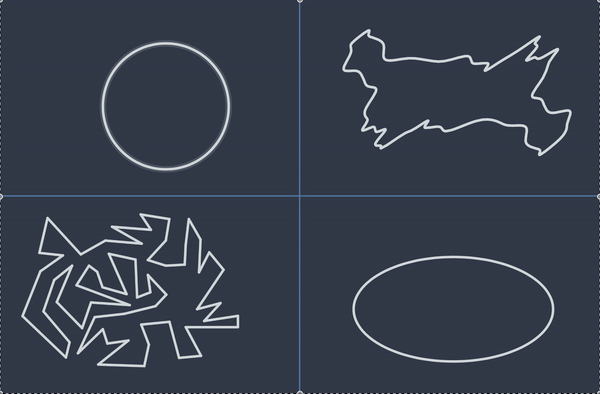
Dado un círculo en el plano ¿Cuántos cuadrados puedes dibujar de tal modo que todos los vértices del cuadrado estén sobre la circunferencia?, ¿y si en lugar de un círculo ahora consideramos una elipse?
¿Puedes encontrar un punto de una elipse que no sea vértice de ningún rectángulo inscrito?, ¿Cuántos puntos con esa propiedad existen en la elipse?
¿Puedes dibujar una curva en el plano que tenga exactamente 4 cuadrados inscritos?
En general uno puede preguntarse por las condiciones que debe satisfacer un conjunto para que inscriba cierto tipo de polígonos, estos son los problemas de inscripción de polígonos. En este sitio encontrarás demostraciones, animaciones, herramientas interactivas y recursos en general, así como una presentación de buena parte de los conceptos necesarios para introducirte en el mundo de los problemas de inscripción de polígonos y sus soluciones.
El sitio está dividido en varias secciones según el tipo de polígono a inscribir. A lo largo de las demostraciones y explicaciones encontrarás que varios términos tienen un enlace que te lleva a la definición y explicación del término en cuestión. Una lista de estos enlaces la encontrarás en la sección “Glosario”
En la sección de “El problema del cuadrado inscrito” encontrarás una reseña del problema más famoso en esta área y que lleva más de 100 años sin resolverse: ¿Toda curva de Jordan inscribe cuadrados?.
En la sección de “Rectángulos inscritos", encontrarás una demostración de que toda curva de Jordan inscribe rectángulos. También presentamos una generalización del problema de inscripción de rectángulos a otro tipo de conjuntos del plano y clasificamos topológicamente a los conjuntos de este tipo que inscriben rectángulos y a los que no.
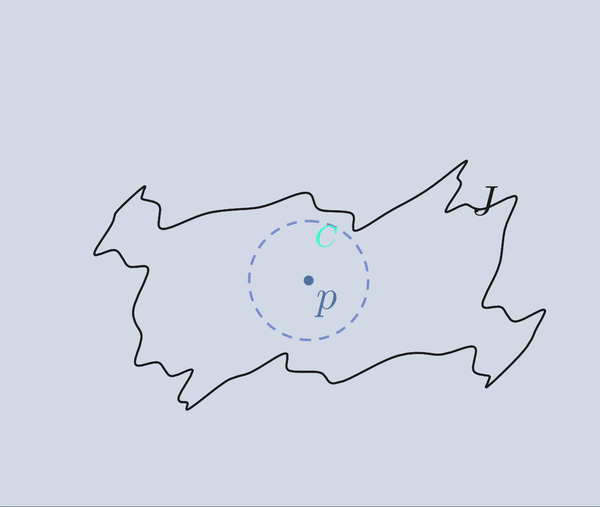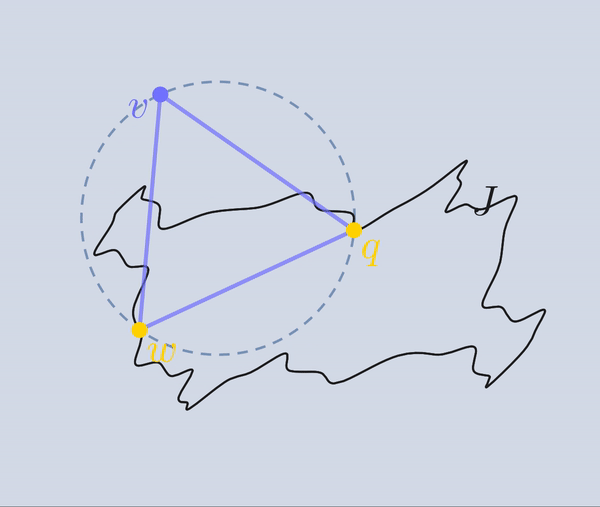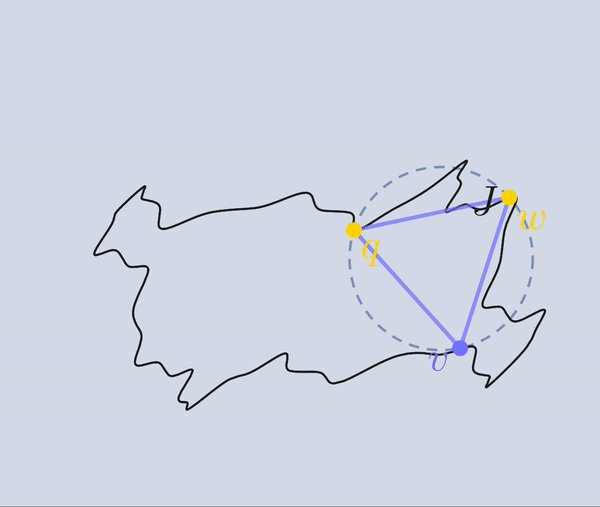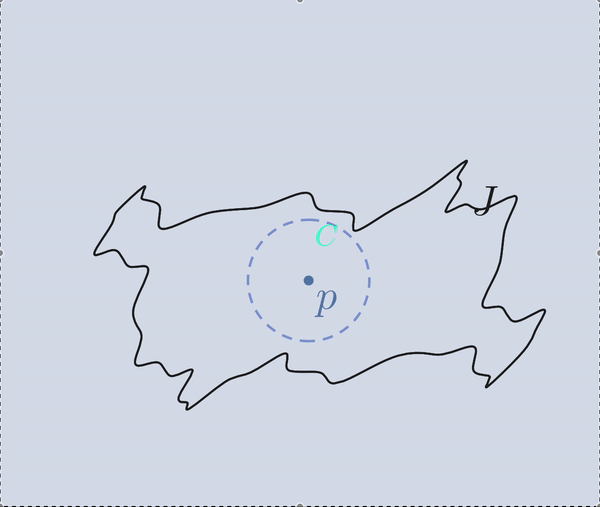
En la sección de “Triángulos inscritos", se expone una prueba de que toda curva de Jordan inscribe triángulos equiláteros.